Gergonne 三角形 の性質

やっと証明できた。

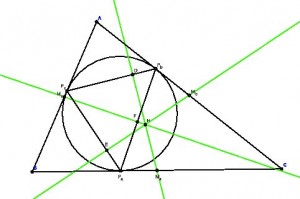
△ABCの内接円と辺BC，CA，ABの共有点をそれぞれP${}_a$, P${}_b$, P${}_c$，
辺BC，CA，ABの中点をそれぞれM${}_a$, M${}_b$, M${}_c$ とする。
このときM${}_a$ から線分 P${}_b$P${}_c$に引いた垂線，M${}_b$から線分P${}_c$P${}_a$に引いた垂線，
M${}_c$から線分P${}_a$P${}_b$に引いた垂線は1点で交わる。

Posamentier & Lehmann, The Secrets of Triangles, Prometheus Books, 2012, p.51　より。