長澤亀之助,「幾何学辞典」の問題1は次のもの。
1. 周角はすべて等しい
「平角はすべて等しい」という定理ならよく見かけるけど。
まず「周角」って何? ってとこからはじまる。
そのために「学語之部」というのがあるのだろう。
早速見てみた。すると,p.489にあって,
周角,Circum-angle,Perigon
角の定義を見よ。
とあった。(適当に現代語訳してあります。以下同じ)
う〜む。
なんとなく気が削がれた。
でも気をとりなおして,「角」の項を見た。p.481
(図もあるのですが,ここのは省略)
角,angle
1点から引いた2つの直線は角をなすといい,
この2つの直線を角の二辺,この1点を角の頂という(頂は「ちょう」と読む)。あるいは,一直線がその一端を枢として回転するときは角を画くという。
角の大きさは辺の長さに関係せず,唯その一辺が他の一辺の位置より回転する
量に関係する。角は時計の針と反対の向きに弧形の鏃を用いて表すのが普通である。
すなわち,角のうちにある1文字をもって表すことができる。
角\(\alpha\) あるいは \(\angle \alpha\) のようである。また角の頂にある1文字をもって表すこともある。角 O あるいは O のようにで
ある。また3文字を用いて表すこともある。
角AOB あるいは AOB のようにである。
ただしこのとき角の頂にある文字を中央におくこと。また,二辺の文字をもって表すこともできる。
角 \((a,\ b)\) あるいは \(\angle (a,\ b)\) のように。直線 OA,OB の間の角とは OA から OB に回転する右回りと左回りの2つある。
それゆえこの2つの角は互いに共役 (Conjugate) であるといい,
大きい方を優角 (Major angle),
小さい方を劣角 (Minor angle) といい,
一直線がその一端を枢として回転し,
再びものと位置にいたるとき画く角を周角 (Circum angle あるいは Perigon)
という。一つの点から3つの直線 OA,OB,OC を引き,
OB が角 AOC の内にあるときは \(\angle\) AOB,\(\angle\) BOC は接角
または隣角 (Adjacent angles) という。
最後の方にようやく出てきた。
で,
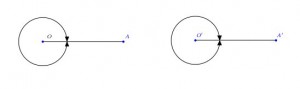
周角OとO\({}^\prime\)はそれぞれ主線OA, O\({}^\prime\)A\({}^\prime\)がO,O\({}^\prime\)を軸として紙面を離れることなく1回転してできる角なので,OをO\({}^\prime\)に重ね,OAをO\({}^\prime\)A\({}^\prime\)に重ねることができるので全く等しい。
よって周角Oは周角O\({}^\prime\)と等しい。
このあたりは,平角の場合と同じ。
でも,最初の問題がこれで,ちょっと度肝を抜かれた。